https://openreview.net/forum?id=dZA7WtCULT
Introduction
Self-supervised LearningではUnlabeledを利用してうまく行くようになるときも、逆に性能が下がってしまう時もある。特に、Domain Shiftが起きているときは性能が逆に下がってしまうことが多い(変なpseudo labelをつけてしまう)
Domain Shiftの例
- LabeledとUnlabeledが違うソースである。
- Labeledが実データだが、Unlabeledが合成データ
- Labeledが人手て集められていて、そこで役に立ちそうだとかなどで選択バイアスが生じている。
Domain Shiftについて、Unlabeledであるという性質上、我々が観測できるのはだけである。だが、これは
- Distribution Shift
- Intra-class Feature Distribution Shift
これの合わせ技と言える。下の図の例として、ラベルの分布がそもそも違う(個数が違う)、同じラベルでもデータの分布が違うということになる。
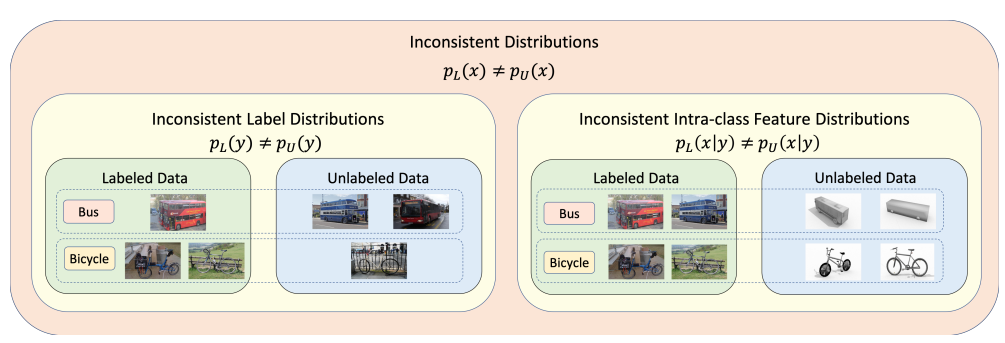
この問題については、Self-supervised Leanringは共変量シフトがない前提なので考慮していない。理論的にはいろんな研究があるが、未だにアルゴリズムレベルで落とし込めてはいない。
この論文では、PositiveとUnlabeledのDomain Shiftを考慮した手法を開発した。先行手法は訓練データで訓練して、pseudo labelを付与するが、テストデータでもそれを適用しようとするのでずれてしまう。他にも、訓練時にはLabelありとLabelなし(重みを調節して)で訓練してしたのに、テストするときはドメインが違うので性能が下がる問題がある。この研究では、以下のようなことがわかった。
- 性能低下を招く3つの要因を特定した
- Pseudo Label生成器と、Test Domainでの識別器が違う。
- Pseudo Labelにバイアスがある。
- サンプルの重みに制限がある
- これらを解決するBidirectional Adaptationを開発。Pseudo Label予測器とTarget予測器を分離し、BiasのないPseudo Label予測器のためにUnlabeledデータの分布に適応し、BiasのないTarget予測器のためにTarget分布に適応する。
- ようわからんので、後を読もう。
Related Work
Robust Self-supervised Learning
Domain Adaptation
違うドメインのデータでも、同じ特徴空間の上でマッピングする、重みを変更するなどをして、ドメインが違くとも学習できることが目標。
基本的に最大平均不一致(MMD)、Wasserstein距離、Contrast Domain Discrepancy
- 最大平均不一致(MMD) 再生核ヒルベルト空間に写像したときの距離を最小化 📄
Distribution Shiftの基礎 にある通り。
- Wassertein距離 最適輸送のコスト行列によって、定義される分布の間の距離。
- Contrastive Domain Discrepancy(CDD) いろいろあるが以下の数式で評価する。はどのドメインからきているかを識別するもので、はそれぞれのドメインからきている。
自己教師あり学習の理論
自己教師あり学習では、仮定を設けない限り教師あり学習を残念ながら超えることができない。逆に言えば、についての効果的な仮定があれば肩を並べられる。
先行研究ではLabeledとUnlabeledの間にDomain Shiftがあることを研究したが、サンプリングによるバイアス=(biased PUのように)だけ考えている。
理論的な結果
問題設定
- サンプルはであり、ラベルはとなる。
- ラベル付けされた個のサンプルの集合は
- ラベルがついてない個のサンプルの集合は
- この論文では、以下の条件を考える。
- 同時分布の見た目は同じように見えるが、サンプルもラベルもズレているので奇跡的にあっている場合。
Natarajan次元
多クラス分類問題においてのVC次元の拡張であるNatarajan次元というものがあり、であるとする。
解説はこちら
Natarajan次元の定義は、仮説空間に対して、個のサンプルについて、ありえるクラスが個あるとき、通りの割り当てができる、という最大のがNatarajan次元である。
はサンプル数、はクラス数、は信頼度で、以上で成り立つという条件。
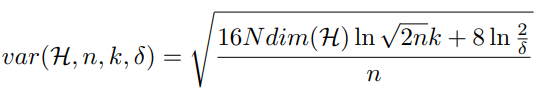
ここでいうは何かしらの確率変数についての分散ではなく、経験誤差と真の識別器による誤差の差について、これ以下に収まるというものである。
つまり、集中不等式で書くと、以上の確率で、以下が成り立つ。
分布の不一致の定式化
2つの分布の間の不一致は、ある識別器を用いて以下のように定式化する。これはDomain Shiftにおける一般的な指標。
分布1と2について識別器の間違える率の差である。ここで間違える率がいかに小さいかは評価されず、いかに同じ間違える率なのかを見られる。
自己教師あり学習の目的
Target Domainにおけるエラーを最小化する識別器を選びたい。ラベルがないデータを使うので、自己教師あり学習はの間の関係を事前知識として与える。
従来の手法は、仮説空間の中から重要ではない関数を除外した上で選ぶか、新たな仮説空間に埋め込んでそれを基準にすることが多かった。
この研究では、ラベルありデータとラベルなしデータの分布が一致しないときでも分析できる理論フレームワークを提案した。Base Learnerという本来のLabeled以外にも、UnlabeledにPseudo Labelを付与してそれも学習に使う学習器のこと。今回はLabeledとUnlabeledの間でDomain Shiftがある前提なので、仮定が完全に正しいとしても、ラベルなしデータをベースに付与したPseudo LabelとLabeledはCovariance Shiftがある。
形式的には、SSLには仮定があり、を使用して仮説空間から擬似ラベル予測器を学習する。この予測器は、擬似ラベル付きラベルなしデータセットを得るのに役立つが、Covariance Shiftがあれば最適なものを学んでも根本的にずれることになる。
また、仕組みとしては訓練済か訓練途上のがあり、それをもとにが決まるということになる。
LabeledとUnlabeledの間が同じ分布の時の理論評価
定理3.1
Unlabeledにpseudo labelを付与する識別器があるとする。だとすると、以上の確率で、以下が成り立つ。(ついでにいえば、以上の確率であるともいえるので)
証明
これについては、分布についてそれぞれ、集中不等式で評価すればよい。いずれも真の損失はと書くことができるので、以下のようになる。
これは絶対値の式なので、2つ目の式の絶対値の中の符号を逆転させることで、がちょうど消える形にできる。よって、いずれの式も成り立つとき上のようになる。
この定理は、2つの同じ分布からサンプルされたデータ集合による誤差上界を評価しているだけ。
定理3.2
識別器と、Pseudo Labelを付与する識別器が同一ではないと考えてみる。だとするとき、以上の確率で以下の式が成り立つ。
は真の分布
はPusedo Label付与器よってラベルを付与した状態での、に対する損失。右辺にあるのは上から説明すると、
- Labeledについてのの損失
- Unlabeledを識別器によってラベル付けしたデータセットについての、の損失
- について、個数がとした上界項
- Labeledについてのの損失(1項目はの損失である)
- について、個数がとした上界項
- について、個数がとした上界項
証明はこちら
自己教師あり学習では、とによって、訓練される。これの合成分布で学習するので、経験損失も合成すればいい。
このように合成したときの上界はとなる。
次に、を作り出すためのについての評価を行う。これは先ほど示したような上界が存在する。これについて全体での寄与は、なので係数を乗じて、期待の式が得られた。
LabeledとUnlabeledの間の分布が異なる場合の評価
サンプリングしたLabeled、サンプリングしたUnlabeled、真の分布がそれぞれ全部違うという考えである。
今までの証明では同じ分布に従っていたので、代入して打ち消しと化することができたが分布が違えば打ち消すことはできず、で考える。
定理3.3
Pseudo Labelを付与する識別器があり、の時、以上の確率で以下の式が成り立つ。
分布の違いがあるとき、という項が追加された。2つの分布における識別器の間違える率の違いということなので、右辺にこれが追加されるのも自然である。
定理3.4
定理3.2のものも、同様にを加えることで分布が違う場合を評価できる。
便宜のために、をで混合させたものだとおく。
識別器と、Pseudo Labelを付与する識別器が同一ではないと考えてみる。だとするとき、以上の確率で以下の式が成り立つ。
これについても適宜Discを加えているだけである。
自己教師あり学習の分析
Domain Shiftを含む自己教師あり学習では、を最小化するのが目標である。
先行研究はどのように最小化を試みたか、そしてその欠点を説明する。
自己教師あり学習の定式化
自己教師あり学習は、Pseudo Labelを付与するか、一貫性のある正則化手法というのが二大方針であった。実はこの両方はとを見つけて、その差を小さくするということと同じらしい。
Pseudo Labelの付与は、をつなげる写像を見つけることが重要である。
- 例えば、Soft LabelをHard Labelにそのまま変換する。指数移動平均で過去の予測結果をEnsembleなど。といえる。
- 一貫性のある正則化手法はをもとに、Adversarial Exampleを提供したり普通にRandAugmentしたりすること。これは拡張をとして、といえる。
- この2つの手法を合わせて。FixMatchがある。Hard Labelへの変換もしているし、データ拡張もしている。
- FixMatchはこちらを参照。
既存の自己教師あり学習の欠点
とを紐づけている
当然といえば当然であるが、紐づけられている。が同じ分布ならば問題がないが、が違う分布になったら、当然性能が下がる。実際以下の式をのように合成させていくと、がすべてを決めることになっていて、が入るので最適化が難しい。
Biasを含むPseudo Label
分布が一致しない場合、から見てでPseudo Label付きはバイアスを含むということになる。を考慮してないから。
制限されたサンプルの重み
分布が違う場合、Sample Selectionによってできるだけ影響が出ないように選んで学習をするということができる。という変換する重みの式を考えたい。(Labeledが真の分布であると仮定している)うまくWeightを調節することによって、のDiscを0に近づけたい。
しかし、先行研究ではサンプルの重みは往々にして閾値によって決定された0か1の値であった(最適化が楽だから)
提案手法
双方向Adaptationというフレームワークを設計した。
とを分離させる
分離させれば、別々に最適化できるようになって楽になる。
Pseudo LabelsのBiasを減らす
Pseudo Label予測器の最適化目的が、理想のを得るようなLabelをつけることである。一方、Unsupervised LearningによるDomain Adaptationは2つのDomainを同じ特徴空間の上でマッピングしようとしているものであり、本質的には同じである。
なので、既存のDomain Adaptationを用いて、を訓練できる。
次に、Unlabeledの分布に合致させた、を学習する。予測器から得られたもののSoft Label、Hard Labelを保存しておく。よく考えるとこれはという操作する。
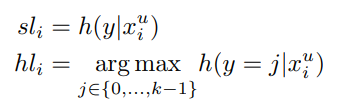
制限されない重み
既存手法はのDomain Shiftを考えていない。
重みを閾値ベースで超える超えないで01に割り振るのをやめましょう。の分布と重なるところの重みを大きく、重ならないところの重みを小さくすることを提案している。
Pseudo Labelを付与された後、を計算できるので、ベイズの定理から一連の計算できる。
をクラス間の重みによる並べ替え
先ほど述べたように、分布と重なる部分の重みを大きく、重ならない部分の重みを軽くしたい。しかし、これは学習しやすいクラスとしにくいクラスがある以上、単純に信頼度を指標にするのは不公平である。
そこで、対象のデータの信頼度と、そのクラスに属するすべてのデータの信頼度を比較することで、ラベル付きデータの分布にどれだけ一致しているのかを測定する=正規化。
ただし、クラス数が多いときはbatch normalizationは効果的ではない。なので、毎回平均をバッチごとに計算するのではなく、今までのそのクラスでの信頼度の平均というものを計算していく。また訓練が進むにつれて信頼度が上がるはずなので、それも加味する。結果としては、以下のようにやる。
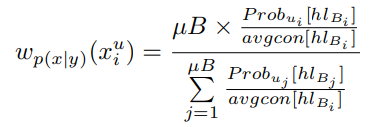
- は当該クラスにおいて過去のBatchを平均した信頼度である。この場合は、すべてHard Labelで平均をとり、
- はUnlabeledのサンプルの予測確率で、Hard Label(つまりそのクラスだと予測されたら1、それ以外は0)
- はバッチサイズ。である(バッチ内の比率)
をクラス間の重みによる並べ替え
各クラスについて、Labeledの中での出現回数を、Pseudo LabelがついているUnlabeledのデータの中での出現回数をとする。
そして、クラス間の重みを以下のように計算する。全クラスのの比と、と逆にしたクラスに限定した比の積である。クラスの比率が、全体よりもLが多いと重みを重くする。
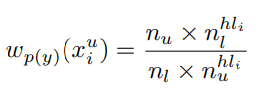
そして、inter-classとintra-class双方の重みを乗じることで、ベイズの定理により、Unlabeledの各サンプルについての重みが得られる。
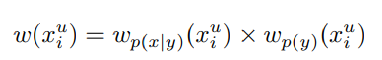
損失関数
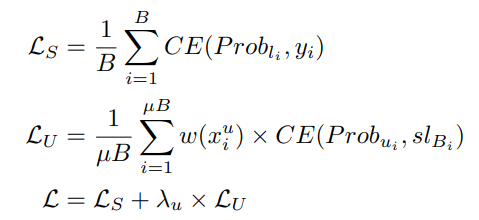
- は通常のラベル付きデータのラベルとによる予測のSoft LabelとのCrossEntropy誤差
- はハイパーパラメタ
- はUnlabeledデータがPseudo Labelを付与されたとき、それぞれの重みについて考慮したうえでの損失。Pseudo Labelで予測されたSoft Labelとで予測されたラベルのCross Entropy誤差である。
全体のアルゴリズム
入力は以下の通り
- は訓練データ。それぞれ個存在する。
- はDomain Adaptation Algorithmで、の写像をしつつ、Pseudo Labelを付与するアルゴリズムだと考えていい。
- イテレーション数、学習率
- クラス数
- バッチサイズ
- 各バッチの中での
出力
- 予測器
- Pseudo Label Giver
h = A(D_L, D_U) # hをまずDAのアルゴリズムで計算する。
for i in range(D_U):
# hによるPseudo Labelを付与
sl_u = softlabel(h(D_U))
hl_u = hardlabel(h(D_U))
for 1 in range(k):
# クラス別の平均やカウントを初期化
avgcon[i] = 0
cnt[i] = 0
for t in range(T):
# Tイテレーション計算する。
# 今の識別器でLとUいずれも予測する。
prob_l = f(D_L)
prob_u = f(D_U)
# mu * Bである理由はわからないが、すべてのD_Uのサンプルに重みを付与している。
for i in ange(mu * B):
compute weight for every sample in D_U.
update avgco and cnt
# 損失の計算
loss = CE(prob_l, D_L.y) + l_lambda * CE(prob_u, sl_u)
backward
updateResult
従来のBaselineとしてのFixMatchとかとも比較した悔過k、こちらの方が性能が良くなった。Labeled, Unlabeledの比率を変更してもこのアルゴリズムは問題を起こさなかった。
